Posts

Implementing Conditional Independence and Understanding RCoT

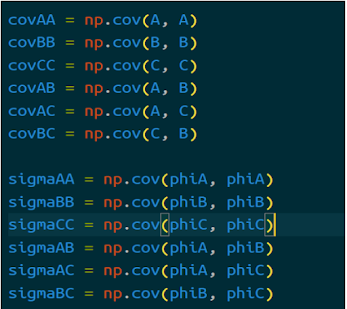
Image
Implemented the Conditional Independence using multiple ways: Using the cross-covariance operator and correlation coefficient Using the Hilbert Schmidt Norm  Reference to Section 2: https://papers.nips.cc/paper/2007/file/3a0772443a0739141292a5429b952fe6-Paper.pdf Since the KCIT method for testing Conditional Dependence has disadvantages of the curse of dimensionality and time taken to process. A good approximation was done on KCIT to improve on the issues and hence RCoT was introduced. I have started to understand and get into the depth of it. Reference: https://arxiv.org/abs/1702.03877 Monday I had been assigned to review the RCot paper and understand the first 2 sections in it. Some notes I made during the review, I have noted below. Kernel independent testing is not time efficient and so it cannot be used for constraint-based conditional independence testing as the data sets in these settings are very huge. 2 options presented by the paper RCoT - Randomized conditional...
Post a Comment
Read more

RKHS Kernel Implementation

Image
 I started my first goal by working on RKHS implementation for understanding the kernel. The main features of it were:  Ability to provide an alternate kernel Ability to provide an alternate Evaluation Method. The “delta” optimization in the Evaluation Method Choosing an Asymmetric kernel Monday I started to explore the concepts of Hilbert Space, inner product, and RKHS. I found some of the important points about it: Hilbert Space is a metric space. Kernel uniquely defines a Hilbert Space, i.e., every Hilbert Space has its own unique kernel. The kernel is symmetric and positive semidefinite function. RKHS is a space of continuous functions. Each point in it represents a function. RKHS includes a reproducing property and has an evaluation function. As we increase the number of points into RKHS, it will converge to the correct solution. The closeness of a Norm is the closeness of the correct solution. Tuesday My internship officially started today with Lexis Nexis. I also contin...
Post a Comment
Read more