RKHS Kernel Implementation

 I started my first goal by working on RKHS implementation for understanding the kernel. The main features of it were: 

• Ability to provide an alternate kernel
• Ability to provide an alternate Evaluation Method.
• The “delta” optimization in the Evaluation Method
• Choosing an Asymmetric kernel

Monday

I started to explore the concepts of Hilbert Space, inner product, and RKHS. I found some of the important points about it:

• Hilbert Space is a metric space.
• Kernel uniquely defines a Hilbert Space, i.e., every Hilbert Space has its own unique kernel.
• The kernel is symmetric and positive semidefinite function.
• RKHS is a space of continuous functions. Each point in it represents a function.
• RKHS includes a reproducing property and has an evaluation function.
• As we increase the number of points into RKHS, it will converge to the correct solution.
• The closeness of a Norm is the closeness of the correct solution.

Tuesday

My internship officially started today with Lexis Nexis. I also continued to learn about RKHS and Hilbert Space. Some of the points that I found to be useful were:

• Every function in RKHS is indexed by data points.
• Representer Theorem: If you do a linear operation in Rd space and replace the inner product with one from Hilbert Space with the RBF kernel, we can then use the same linear regression formula by replacing the Euclidean Space with RBF Kernel.
• Because of the reproducing property of RKHS, linear spaces behave similar to Euclidean space and therefore we can use the linear functions.
• With the help of linear regression, we can find the function which is a linear combination of the distribution.

Wednesday

I had my first 1:1 meeting with my mentor and an amazing guide for me Roger Sir. We had a discussion on the week's plan and the learning I did in the previous 2 days. Sir, guided me into the implementation of my learning into code. The purpose of implementing the RKHS kernel is to predict a probability distribution function for a given distribution of finite sets. This implementation is very useful in understanding RKHS  and is helpful in the implementation of more complex kernels.

Thursday

Started the implementation of RKHS with the RBF Kernel and Evaluation Function. I used the logistic distribution with a mean and scale value as parameters for the distribution and the sigma value as the parameter for the RKHS class.

• F(X) is the Evaluation Function for the RKHS 
• X as an index into RKHS that returns the function F(x).   
• Calling F(x) is the result of that indexed function.  
• So it is the output from the RKHS.

Algorithm:

Class RKHS:

          Def __init__(self, mydata):  # Constructor for the RKHS

                         Self.data = mydata

 

          Def K(x1, x2=0, sigma=1.0): # My kernel function

                         # Kernel code goes here, and uses self.data to do its calculation

                         Return result # A scalar

 

          Def F(x): # My evaluation function

                         # Average all of the results of K(x, Xi) for each Xi in self.data.

                         Return result # A scalar.  This will now be the approximation of CDF(D(x)

Friday

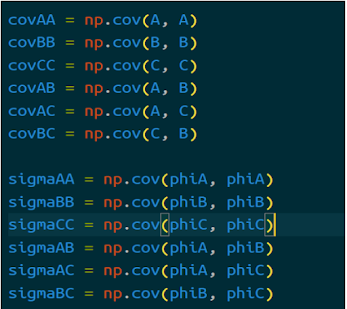
Implemented the code as per the algorithm with the model used for testing:

References

[1] Manton, Jonathan H; Amblard, Pierre-Olivier (2015) "A Primer on Reproducing Kernel Hilbert Spaces", Foundations and Trends in Signal Processing. URL:  https://arxiv.org/pdf/1408.0952.pdf

[2] Sriperumbudur, Bharath K.; Gretton, Arthur; Fukumizu, Kenji; Lanckriet, Gert; Scholkopf, Bernhard (2008) "Injective Hilbert Space Embeddings of Probability Measures", Conference on Learning Theory, URL: http://www.learningtheory.org/colt2008/papers/103-Sriperumbudur.pdf.

[3] Smola, Alex; Gretton, Arthur; Song, Le; Scholkopf, Bernhard (2007) "A Hilbert Space Embedding for Distributions", URL: http://www.gatsby.ucl.ac.uk/~gretton/papers/SmoGreSonSch07.pdf. 

General Causality:

[1] Pearl, Judea (2000, 2008) "Causality: Models, Reasoning, and Inference", Cambridge University Press

[2] Pearl, Judea; Mackenzie, Data (2020) "The Book of Why: The new Science of Cause and Effect", Basic Books

[3] Pearl, Judea; Glymour, Madelyn; Jewell, Nicholas P. (2016) "Causal Inference in Statistics", Wiley

[4] Rosenbaum, Paul R. (2017) "Observation and Experiment:  An Introduction to Causal Inference", Harvard University Press.

[5] Halpern, Joseph Y. (2016) "Actual Causality", MIT Press.

Conditional Independence Testing:

[6] Li, Chun; Fan, Xiaodan (2019) "On nonparametric conditional independence tests for continuous variables" , Computational Statistics, Wiley.  URL: https://onlinelibrary.wiley.com/doi/full/10.1002/wics.1489

[7] Strobl, Eric V.; Visweswaran, Shyam (2017) "Approximate Kernel-based Conditional Independence Tests for Fast Non-Parametric Causal Discovery",  URL: https://arxiv.org/pdf/1702.03877.pdf

[8] Zhang, K.; Peters, J.; Janzing, D.; Scholkopf, B. (2011) "Kernel-based conditional independence test and application to causal discovery", Uncertainty in Artificial Intelligence, p 804-813.  AUAI Press.

[9] Fukumizu, K.; Gretton, A.; Sun, X.; Scholkopf, B. (2008) "Kernel measures of conditional dependence", Advances in Neural Information Processing Systems, p 489-496, URL: https://papers.nips.cc/paper/2007/file/3a0772443a0739141292a5429b952fe6-Paper.pdf

Directionality:

[10] Hyvarinen, Aapo; Smith, Stephen M. (2013) "Pairwise Likelihood Ratios for Estimation of Non-Gaussian Structural Equation Models.", Journal of Machine Learning Research 14, p 111-152.

[11] Shimizu, Shohei (?) "LiNGAM: Non-Gaussian methods for estimating causal structures", The Institute of Scientific and Industrial Research, Osaka University, URL: http://www.ar.sanken.osaka-u.ac.jp/~sshimizu/papers/Shimizu13BHMK.pdf

Causal Discovery:

[15] Glymour, Clark; Zhang, Kun; Spirites, Peter (2019) "Review of causal discovery methods based on graphical models", Frontiers in Genetics; Statistical Genetics and Methodology,  URL: https://www.frontiersin.org/articles/10.3389/fgene.2019.00524/full