Implementing Conditional Independence and Understanding RCoT

Implemented the Conditional Independence using multiple ways:

• Using the cross-covariance operator and correlation coefficient
• Using the Hilbert Schmidt Norm 

Reference to Section 2: https://papers.nips.cc/paper/2007/file/3a0772443a0739141292a5429b952fe6-Paper.pdf

Since the KCIT method for testing Conditional Dependence has disadvantages of the curse of dimensionality and time taken to process. A good approximation was done on KCIT to improve on the issues and hence RCoT was introduced. I have started to understand and get into the depth of it.

Reference: https://arxiv.org/abs/1702.03877

Monday

I had been assigned to review the RCot paper and understand the first 2 sections in it. Some notes I made during the review, I have noted below.

Kernel independent testing is not time efficient and so it cannot be used for constraint-based conditional independence testing as the data sets in these settings are very huge.

2 options presented by the paper

• RCoT - Randomized conditional Correlations Testing
• RCIT - Randomized Conditional Independence Testing

Both Approximate KCIT using Random Fourier Features.

Tuesday

Continued to study the RCot paper and also implementing the 2nd Task which is to implement the kernel conditional independence test in python. The formulas for this are present in the KCIT paper which I reviewed today.

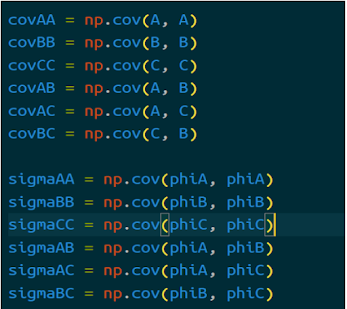
I was able to complete creating a new model to test out the conditional independence and work with it to calculate the variance and covariance of all the random variables.

Wednesday

Finished implementing conditional independence code by calculating the correlation between

the random variables in our model.

Sir suggested that I use the iceCream model to test out the code. I tried implementing that and

we had a discussion of our further steps in the 1:1 meeting.

For the next week plans discussed with Roger sir: I have been assigned to start working on

RCot code and its use of KCIT. It will involve reading through an understanding section 3 of

RCot paper.

Thursday

After presenting to Roger Sir on Wednesday, I went on to do some updates and make changes

to the code to make it more clear and tried more variations with the model and added more

complexities to it, and tried to interpret the results. I also added dependence to more than one

variable and tested it. The model is given below:

The output of Unconditional Dependence and Conditional Dependence that I got after adding

more dependence and variations to the model are shown below:

Friday

After testing with Equation 3 of the Fukumizu 2008 paper for calculating the conditional

dependence, I started working with one more way for calculating the conditional dependence

with the concept of Hilbert Schmidt Norm:

Where X(dot) is a combination of (X,Z) taken together and Y(dot) is a combination of (Y,Z) taken

together and then calculates the V as per the equation3 and finally calculates the Conditional

Dependence with the Hilbert Schmidt Norm of V.

I tested all the models I generated earlier for Equation 3 checking with Hilbert Schmidt Norm to

see the accuracy of the results as per the model. The output is shown below:

When compared the results of Hilbert Schmidt with Equation 3, I found that Equation3 gave

better results

Saturday

After testing the models, I was unable to figure out certain results which were not depicting the

a clear understanding of the difference between covariance, correlation, and independence.

So, I went back to some concepts and tried to understand them. While reading through different

articles and sections of some papers, I found some simple but important interpretations between

the multiple concepts and terminologies. I mentioned below:

• Covariance depicts only the directionality of the linear relationship between the random variables, not the strength. So, anything above zero meant only positive covariance means they change in tandem and anything below zero meant that it shows an inverse relationship.
• Correlation depicts the strength of a relationship. The absolute value of correlation meant how strongly the random variables are related to each other irrespective of the direction.
• If X and Y are independent the covariance(X,Y) = 0. But the converse if false i.e., the(X, Y)=0 does not imply that X and Y are independent.

I also implemented a more complex model to test conditional dependence.

The outputs are shown respectively:

Next Week Plans

• Working on the multiple conditional variables.
• Going forward with RCOT paper (Test Statistic - Section 3)
• What approximation is done on KCIT which results in RCOT